Applied Mathematics 2021 — CSS Past Paper
FEDERAL PUBLIC SERVICE COMMISSION
COMPETITIVE EXAMINATION-2021
FOR RECRUITMENT TO POSTS IN BS-17
UNDER THE FEDERAL GOVERNMENT
APPLIED MATHEMATICS
TIME ALLOWED: THREE HOURS
PART-I(MCQS): MAXIMUM 30 MINUTES
PART-I (MCQS) MAXIMUM MARKS = 20
PART-II MAXIMUM MARKS = 80
NOTE:
- (i) Attempt ONLY FIVE questions from PART-II. ALL questions carry EQUAL marks.
- (ii) All the parts (if any) of each Question must be attempted at one place instead of at different places.
- (iii) Candidate must write Q. No. in the Answer Book in accordance with Q. No. in the Q.Paper.
- (iv) No Page/Space be left blank between the answers. All the blank pages of Answer Book must be crossed.
- (v) Extra attempt of any question or any part of the attempted question will not be considered.
- (vi) Use of calculator is allowed.
PART-II
Note: Each question caries 20 marks which are subdivided in to sub parts a and b; which are 10 marks each part.
Q. No. 1.
(a) Evaluate the surface integral ff A. ildS where A = zi + xj — 3y2zk and S is the portion of the cylinder x2 + y2 = 8 lying in the first octant between z = and z = 4.
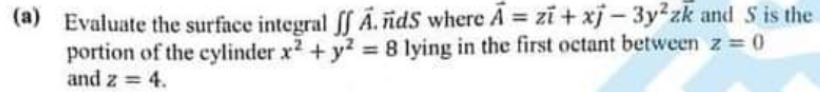
Applied Mathematics Question No. 1 a CSS 2021
(b) Prove that
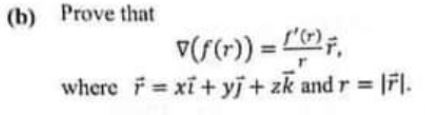
Applied Mathematics Question No. 1 b CSS 2021
Q. No. 2.
(a) The greatest resultant that two forces can have is of magnitude P and the least is of magnitude Q.Show that, when they act at an angle a, their resultant is of magnitude
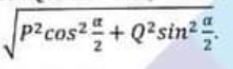
Applied Mathematics Question No. 2 a CSS 2021
(b) A sphere of weight W and radius a is suspended by a string of length 1 from a point P and a weight w is also suspended from P by a string sufficiently long for the weight to hang below the sphere. Show that the inclination of the first string to the vertical is
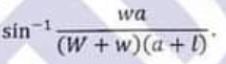
Applied Mathematics Question No. 2 b CSS 2021
Q. No. 3.
(a) Show that the law of force towards the pole, of a particle describing the curve
r” = a” cosnO
Applied Mathematics Question No. 3 a CSS 2021
is given by
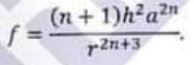
Applied Mathematics Question No. 3 aa CSS 2021
(b) The maximum velocity that a particle executing simple harmonic motion of amplitude a attains, is v. If it is disturbed in such a way that its maximum velocity becomes nv. Find the change in the amplitude and the time-period of motion.
Q. No.4.
Define ordinary and singular points of the differential equation a2(x)y”+ as(x)y’ + oo(z)y = 0.
When a singular point is said to be regular and irregular? Find regular and irregular singular points of the differential equation
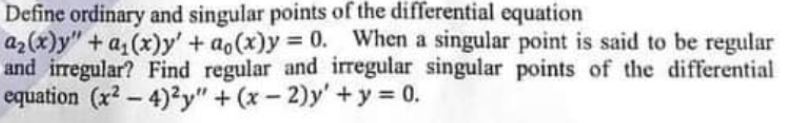
Applied Mathematics Question No. 4 a CSS 2021
(b) Show that
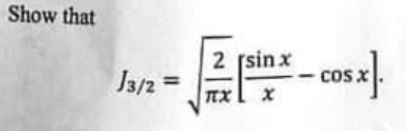
Applied Mathematics Question No. 4 b CSS 2021
Q. No. 5.
(a) Solve the equation by using method of undetermined coefficient
Applied Mathematics Question No. 5 a CSS 2021
(b) Use the method of Frobenius to find two linear independent series solutions in Powers of x of the DE.
Applied Mathematics Question No. 5 b CSS 2021
Q. No. 6.
(a) Classify general second order partial differential equation (PDE) into elliptic. parabolic and hyperbolic form. Discuss the nature of the PDE.
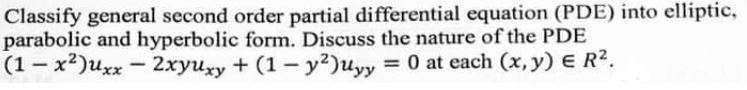
Applied Mathematics Question No. 6 a CSS 2021
(b) Use the method of separation of variables to find the solution

Applied Mathematics Question No. 6 b CSS 2021
Q. No. 7.
(a) Use Simpson’s 3/8 rule to estimate the integral
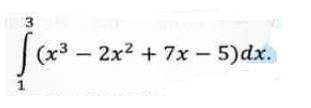
Applied Mathematics Question No. 7 a CSS 2021
f(x3 — 2×2 + 7x — 5)dx.
By comparing your answer with exact value, find the error.
(b) Solve the system of equations by Jacobi iterative method.
10x + 3y + z = 19,
3x + 10y + 2z = 29,
x + 2y + 10. = 35
Q. No. 8.
(a) In the following table values of y = x + sin x2 are tabulated
| X | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 |
| F(x) | 1.84147 | 2.03562 | 2.19146 | 2.29290 | 2.32521 | 2.27807 | 2.14935 |
Construct a difference table and estimate f (1.04) and f (1.57).
(b) Use trapezoidal and Simpson’s 1/3 rules to approximate
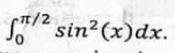
Applied Mathematics Question No. 8 b CSS 2021
Find a maximum bound for the error in each case. Compare your approximations with the actual result.
**********