Pure Mathematics 2021 — CSS Past Paper
FEDERAL PUBLIC SERVICE COMMISSION
COMPETITIVE EXAMINATION-2021
FOR RECRUITMENT TO POSTS IN BS-17
UNDER THE FEDERAL GOVERNMENT
PURE MATHEMATICS
TIME ALLOWED: THREE HOURS
PART-I(MCQS): MAXIMUM 30 MINUTES
PART-I (MCQS) MAXIMUM MARKS = 20
PART-II MAXIMUM MARKS = 80
NOTE:
- (i) Attempt ONLY FIVE questions from PART-II. ALL questions carry EQUAL marks.
- (ii) All the parts (if any) of each Question must be attempted at one place instead of at different places.
- (iii) Candidate must write Q. No. in the Answer Book in accordance with Q. No. in the Q.Paper.
- (iv) No Page/Space be left blank between the answers. All the blank pages of Answer Book must be crossed.
- (v) Extra attempt of any question or any part of the attempted question will not be considered.
- (vi) Use of calculator is allowed.
PART-II
SECTION-A
Q. No. 1.
(a) Let ‘y’ be a homomorphism of group G into group G with kernel K. pros e that K is a normal subgroup of G. (10)
(b) Prove that if H and K are two subgroups of a group G, then HK is a subgroup of G if and only if HK-K1-1.
Q. No. 2.
(a) Find elements of the cyclic group generated by the permutation.
a = (1 2 3 4 5 6)
3 4 5 2 6 1 )
(1(,)T (10) (20)
(b) Verify that the polynomials 2-x^2, x^3-x, 2-3x^2 and 3-x^3 form a basis for the net the set of all polynomials of degree three. Also express the vectors 1+x2 and x+x^3 as a linear combination of these basis vectors.
Q. No. 3.
(a) Let V be the real vector space of all function from R to R. Show that (cos^2 x, sine^2 x, cos 2x) is linearly dependent while {cos, sins, coshx, sinhx} arc linearly independent. (10)
(b) Solve the system of linear equations: (10) (20)
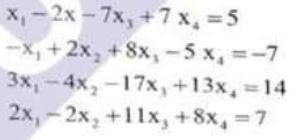
Pure Mathematics, Q No. 3, b, CSS 2021
SECTION-B
Q. No. 4.
If
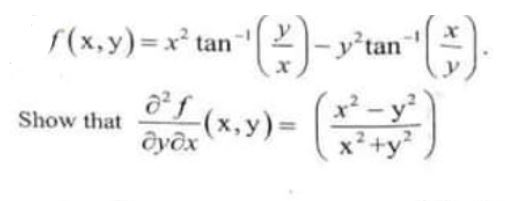
Pure Mathematics, Q No. 4, a, CSS 2021
Show that.
It / (x,y)= tan-1(.0- y2tan-I(‘-:::). Show that -2-1-(x, y) ayax x +y whenx < 2 (r)
(b) Evaluate
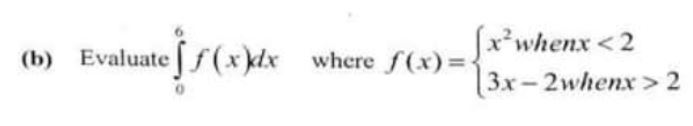
Pure Mathematics, Q No. 4, b, CSS 2021
Q. No. 5.
(a) Let
where n is an integer. Prove that
Hence show that
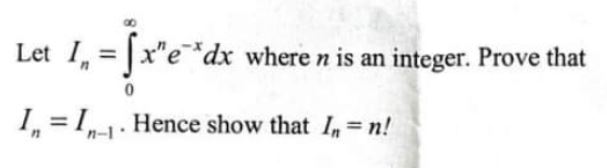
Pure Mathematics, Q No. 5, a, CSS 2021
(b)
-
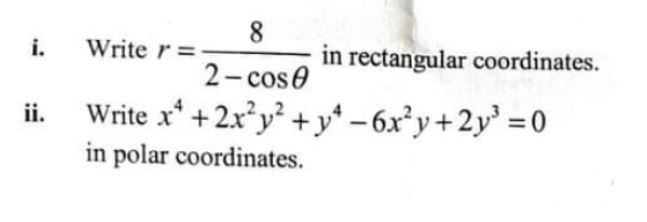
Pure Mathematics, Q No. 5, b, CSS 2021
Write r = in rectangular coordinates. 2 — cos 9
- Write x4 + 2x2y2 + y4 — 6x2y + 2y2 = 0 in polar coordinates.
Q. No. 6.
Evaluate
if dydx and ffaxd’.
where D is the region bounded by the y-axis, the lines x=2 and the curve e’.
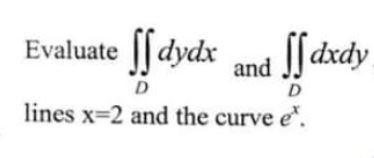
Pure Mathematics, Q No. 6, a, CSS 2021
(b) Investigate the curve y = 3×2 + ]for points of inflexion.
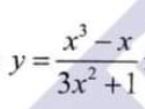
Pure Mathematics, Q No. 6, b, CSS 2021
SECTION-C
Q. No. 7.
(a) Sum the series
1 + 1/2 —cos 0 + 1.3/2.4— cos 20 + 1.3.5/2.4.6— cos30 + …
(b) Prove that
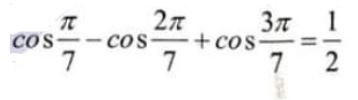
Pure Mathematics, Q No. 7, b, CSS 2021
Q. No. 8.
(a) Construct the analytic function f whose real part isU = .x3 — 3xy2 +3x + 1 (10) (10) (20)

Pure Mathematics, Q No. 8 a, CSS 2021
(b) Evaluate
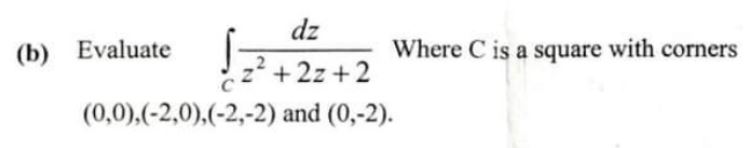
Pure Mathematics, Q No. 8, b, CSS 2021
Where C is a square with corners z2 + 2z + 2 (0,0),(-2,0),(-2,-2) and (0,-2).
**********